

먼저 배경부터 말씀드리겠습니다. 캐싱 테크닉은 클라우드 컴퓨팅 분야에서 널리 사용된다고 합니다. 캐시 데이터를 예측하는 것은 캐시 management와 hit rate를 높일 수 있다고 합니다. 그리고 최근 딥러닝 기술의 발전으로 새로운 intelligent cache replacement policy를 디자인 할 수 있다고 합니다.
그리하여 본 논문에서 미래 데이터 액세스를 예측하기 위한 learning-aided approach를 제안합니다. 이는 powerful LSTM-based RNN로 구성할 것입니다. 왜냐하면 Powerful LSTM based RNN이 높은 정확도로 예측할 수 있다는 것을 발견했기 때문입니다. 이러한 높은 정확도는 carefully crafted locality-driven feature design 덕분이라고 합니다. Locality driven feature은 3장에서 설명합니다.
결론적으로 높은 정확도에 영감을 받아 pOPT를 제안하고 마이크로소프트 클라우드의 13개 실제 스토리지 워크로드에 대해 평가한다고 합니다. pOPT는 최첨단 practical policies에서 최대 19.2% 향상시키는 반면 평균적으로 OPT보다 2.3% 높은 미스 비율만 발생시킨다는 것을 보여줍니다.
INTRODUCTION

캐시는 컴퓨터 과학에서 굉장히 중요한 분야라고 합니다. 왜냐하면 1%의 캐시 적중률의 증가가 35%의 latency를 줄이기 때문이라고 합니다.
그리고 논문에서 중요하게 다루어지는 여러 개념들이 나오는데요. 먼저 reuse interval입니다. Reuse interval의 정의는 같은 데이터에 대한 2개의 연속적인 접근 사이의 접근의 수라고 합니다. 이는 이후 For example 부분에서 자세히 설명될 것입니다. Cache trace는 캐시 접근의 시퀀스라고 하고요. 2개의 reuse interval 타입이 있다고 합니다 하나는 backward reuse interval이고요. 다른 하나는 forward reuse interval이라고 합니다.
그리고 For example 부분에서 reuse interval이 무엇인지 설명됩니다. 먼저 a1b1a2b2a3a4b3이 있을 때, ai는 a의 i번째 등장이라고 합니다. 그리고 b2를 볼 때 forward reuse interval은 3이고 backward reuse interval은 2라고 합니다. 왜냐하면 b2 다음에 나오는 b3 사이에 3개의 원소가 있고, b2와 b1사이엔 2개가 있기 때문입니다. backward reuse interval은 reuse interval로 줄여 쓴다고 합니다. 그리고 참고로 첫번째 데이터는 backward reuse interval은 무한이라고 합니다. 왜냐하면 이전에 나오는 원소가 없으니까요. Last access의 forward reuse interval이 무한인 것도 마찬가지의 이유입니다.

Forward reuse interval을 아는 것이 굉장히 중요하다고 합니다. 왜냐하면 OPT는 향후 오랫동안 필요로 하지 않는 데이터를 삭제하기 때문입니다. 그러나 online computation은 미래가 볼 수 없기 때문에 forward reuse interval은 불가능하다라고 합니다.
그래서 본 논문은 새로운 learning-aided approach로 과거 cache trace만을 활용하여 forward reuse interval을 예측하고자 합니다. 그리고 캐시 replacement분야에서 approach의 강점을 입증하려고 하고요.
그렇게 하기 위하여 RNN으로 forward reuse interval의 오차를 줄이려고 하는 것이 이 논문의 목표입니다.
*proof-of-concept: 아이디어가 현실로 바뀔 수 있는지 여부를 결정하는 데 작업이 집중되는 연습

그리고 forward reuse interval을 예측하는데 있어 높은 정확도와 가용성을 입증하려고 하고, cache trace를 기반으로 한 예측이 실행 가능한지 확인하려고 합니다. 그래서 pOPT라는 새로운 cache replacement policy를 제시합니다. 결론적으로 최첨단 practical policies를 19.2% 향상시키는 동안 opt보다 2.3%만 높은 미스 비율을 발생시켰다고 합니다.
BACKGROUND

그리고 배경부분입니다. Stack distance와 reuse interval을 다루는 부분인데 요. 먼저 stack-distance란 동일한 데이터 블록에 대한 두 개의 연속적인 액세스 간의 고유 액세스 수라고 합니다. 예를 들어 a2와 다른 데이터 a 사이에 2개의 b, c라는 다른 데이터 블록이 있으므로 stack distance는 2입니다.
이러한 stack distance는 MRC라는 miss ratio curve에서 캐시 사이즈에 대한 캐시 미스 비율을 계산하는데 사용할 수 있습니다. 그리고 stack distance와 마찬가지로 reuse interval를 사용하여 volume fill time을 통해 MRC를 계산할 수 있다고 합니다.
Volume fill time은 캐시를 어떠한 크기까지 채우는데 프로그램이 걸리는 시간입니다. 이Volume fill time metric으로, 미스 비율도 쉽게 계산할 수 있다고 합니다.

이 장은 RNN관련 부분입니다. RNN은 sequential prediction을 해결하는데 큰 성공을 커두었다고 하여 이 논문에서 LSTM을 통해 reuse interval을 예측한다고 합니다.

이번 장은 RNN에 대한 이야기입니다. Hidden state, input gate, forget gate, output gate에 대한 내용입니다. 그리고 다음 장과 같은 공식이 사용된다고 합니다.

여기서 [xt , ht−1]는 현재 입력과 이전의 숨겨진 상태의 연결을 나타내고, ⊙는 원소별 곱셈을 나타내며, 이 부분은 sigmoid 방법입니다. 위 과정은 단일 LSTM 셀의 작업 메커니즘을 묘사한다. 완전한 LSTM모델은 계단 식으로 하여 수십 개의 셀들로 형성됩니다. 이러한 LSTM은 long term sequences를 기억하며 sequence to sequence 매핑에도 사용할 수 있습니다. Caching probnlems는 이미 해결된 sequence problems와 같기 때문에 LSTM based RNN을 사용하여 forward reuse interval을 학습합니다.
RNN MODEL DESIGN

RNN은 sequence-to-sequence machine translation 문제에서 큰 성공을 보여주었으며, forward reuse interval의 prediction은 시퀀스 대 시퀀스 문제로 간주될 수 있습니다

Multi-LSTM RNN 모델의 예입니다. 시간 T-1까지의 예측을 마쳤고 시간 T에 대하여 예측을 하고 있다고 합니다. 그리고 train후 256차원 tensors를 출력한다고 하고 이를 단일 single floating point value로 바꾼다고 합니다. LSTM Layers의 수는 하이퍼 파라미터 라고 합니다. 그리고 다음 장에서 자세히 설명합니다.

여기서 stacked LSTM-based RNN model을 사용합니다. 그리고 LSTM에 대한 전반적인 내용이 나와있습니다. 각 스텝에서 이전 hidden state에서 1차원 feature tensor를 읽고 output tensor를 생성하여 다음 hidden state로 넘기고, 레이어는 새로운 텐서 시퀀스를 생성하고 그것을 다음 레이어에 시퀀스를 공급하는 등 전반적인 lstm에 대한 내용이 나와있습니다.

그리고 Lstm이 longterm data dependency(이미 수행된 데이터의 변화가 뒤의 수행 결과에 영향을 끼치는 것을 의미한다)를 포착한다는 것을 보여주고 gru또한 데이터 dependency를 포착하여 lstm과 gru는 비슷한 성능을 보인다고 합니다

이 부분은 lstm이 임베딩을 통해 feature value를 축소하는 것과 그것을 lstm layer에 주는 것, one floating point value Yt로 축소하는 것 forward reuse interval또한 축소하는 것을 나타냅니다.
Locality-Driven Feature Design
이제 Locality-Driven Feature Design에 대한 내용입니다. 이 문단은 LRU나 ARC같은 다른 캐시 replacement policies와 비교합니다. 먼저 cache trace에서 feature을 추출하고, cache trace에서 각 엑세스는 feature tensor에 해당합니다. LRU는 data recency를 LFU는 데이터 빈도를 cache replacement를 할 때 고려합니다.
이후 페이지에서는 여러 feature에 대하여 설명할 것입니다.
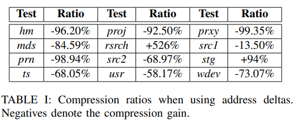
Address delta입니다. 이는 데이터 주소 정보에 관한 것입니다. 이게 왜 쓰이냐 하면, 스토리지 캐시의 경우 메모리 주소 범위가 매우 넓을 수 있고, 이럴 때 LSTM의 훈련 능력이 떨어지기에 주소 정보를 압축하여 나타내기 위해 address delta를 사용하도록 합니다. Address delta 사용 시 각 액세스에 대하여 현재 주소와 이전 주소의 차이를 계산하는 데, 이렇게 하면 고유한 address delta가 줄어들어 lstm 훈련능력이 떨어지지 않을 것이라 추측됩니다. 위 table 1은 압축 비율을 나타냅니다.
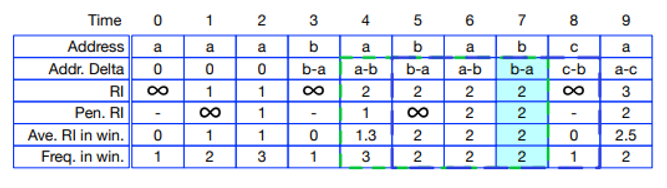
다음은 reuse interval입니다. 앞서 설명했으니 넘어가겠습니다
이번에는 패널티멧 reuse interval입니다. 패널티멧은 끝에서 두 번째의 라는 뜻을 가진 단어고요. 이는 데이터의 마지막 액세스와 동일한 데이터의 마지막 액세스 사이의 액세스 수로 정의됩니다. 즉 마지막 2번째 backward reuse interval이라고 이해하시면 됩니다. 이 기능은 reuse interval이외에도 데이터 recency를 강화하기에 사용됩니다.
슬라이딩 윈도우를 사용하는 average reuse interval입니다. 슬라이딩 윈도우의 개념을 알면 쉽게 이해할 수 있는 부분입니다. 특징은 ‘specific’한 forward reuse interval을 예측해야 하므로 parameter k가 작은 것이 바람직 하다 합니다. 물론 k가 전체범위라면 정확한 average reuse interval을 계산할 수 있겠지만 슬라이딩 윈도우를 사용하는 이점이 없어질 것입니다.
이 부분은 sliding window의 frequency입니다. 이름그대로 silding window의 frequency입니다.
Features 부분에 대한 설명을 마쳤고, 이 챕터는 reuse interval prediction은 분류문제 인지 회귀문제인지에 대한 문제를 다루고 있습니다. 결론적으로는 회귀문제라고 합니다. 왜냐하면 forward reuse interval은 범위가 무한대라 범주 수가 제한 되지 않으면 예측이 불가능 하고, 적은 수 카테고리 만을 예측할 때 큰 오류가 발생할 수 있으므로 회귀라고 합니다.
PREDICTION-BASED PSEUDO OPT
이전에 언급했 듯 Opt는 가장 오랫동안 사용되지 않을 데이터 블록을 폐기합니다. 그리고 신경망 훈련 후, cache trace를 통해 모든 액세스의 forward reuse interval을 예측합니다. 모든 액세스에 대하여 forward reuse interval을 예측하고, 그것을 사용하여 예측기반 pseudo OPT policy를 구현하고 이를 pOPT라고 합니다.

알고리즘 1은 pOPT 정책을 제시합니다. 입력에는 길이 N의 캐시 트레이스, 사전 훈련된 모델 TM 및 크기 C의 캐시가 포함됩니다. 출력은 pOPT 캐시를 통해 실행되는 지정된 trace의 미스 비율입니다. 그리고 캐시를 구현하기 위해 해시 테이블을 사용합니다. 해시 테이블의 키는 데이터 블록이며, 값은 캐시 제거에 사용되는 캐시 엔트리의 다음 액세스 시간입니다. 또한 다음 액세스 시간이 가장 먼 데이터 블록을 신속하게 반환하기 위해 우선 순위 목록을 유지합니다. 우선 순위 목록은 다음 액세스 시간을 기준으로 모든 데이터 블록을 정렬하는 최대 힙으로 구현됩니다.
라인 하나하나에 대하여 설명하겠습니다. 먼저 line 5입니다. Algorithm 1의 3을 보시면 됩니다. 여기서는 모든 데이터 액세스를 반복하고, 각 액세스를 따라, feature tensor를 계산 후, 샘플을 구성하고 얻어진 예측된 forward reuse interval을 신경망에 feed할 수 있습니다. Line 10 즉 algorithm 1의 8은, 다음 액세스 시간이 0인지 여부를 검사하여 액세스 중인 데이터 블록이 이미 캐시에 있는지 여부를 검사합니다. 다음 액세스 시간이 0이면 데이터 블록이 저장되지 않음을 나타냅니다. 데이터 블록이 캐시에 저장되지 않으면 결측 값이 증가하기에 중요한 라인입니다. 캐시가 가득 차면 13번 라인은, 즉 알고리즘 1에서 11, 현재 데이터 블록을 삽입하기 위해 앞으로 가장 오랫동안 액세스하지 않을 캐시 엔트리를 제거하고. 라인 14 즉 알고리즘 1에서 12번째 줄은 현재 블록의 다음 액세스 시간을 삽입하거나 업데이트합니다.
시간복잡도는 lstm 모델의 inference operation의 시간복잡도에 따라 달라집니다. 시간 복잡도는 O(max(log(C))(log c의 최대 값)이라고 하고요. 공간 복잡도는 단순히 o©라고 합니다
EVALUATION
evaluation부분이고 이 섹션에서는 proposed 된 apporach의 예측 정확도와 pOPT의 미스 레이트 성능을 평가한다고 합니다
Cache policies 부분부터 설명합니다.
먼저 pOPT가 2Q, ARC, DRRIP, opt, 그리고 최근 개발된 하나의 딥 러닝 기반 정책인 패럿등의policy와 비교된다고 합니다. 그래서 이 문단에서는 다른 policy들에 대한 대략적인 설명이 주가 됩니다.
LRU는 가장 최근에 액세스한 데이터 블록을 대체하여 데이터 최근을 캡처하고 데이터 주파수를 사용하지 않는 policy라고 합니다. LFU는 최근 데이터를 사용하지 않고 데이터 frequency만 사용하므로 자주 액세스하지만 더 이상 사용되지 않는 오래된 데이터 블록을 캐시에 축적할 수 는 policy라고 합니다. 나중에는 많은 캐시 policy들이 LRU와 LFU를 기반으로 개선하려고 노력합니다
LRU-K는 reference에 대한 재사용 간격을 추정하기 위해 마지막 K reference의 시간을 추적함으로써 데이터 recency를 고려하면서 LFU를 근사화한다. 구현에는 로그 시간 복잡성이 필요합니다. 2Q는 LRU-2를 모방하지만 time 오버헤드가 일정하므로 pOPT를 2Q와 비교한다. ARC는 학습 규칙을 사용하여 데이터 recency와 온라인 frequency 간의 균형을 맞춰 캐시 action을 조정하며, 가장 성능이 좋은 실용적인 정책 중 하나로 알려져 있습니다. ARC는 생산 시스템에서 광범위하게 사용됩니다. DRRIP는 캐시 블록당 2비트만 사용하여, cache trace cases에 대한 scanresistant and thrash-resistant를 하여 course-grained reuse interval을 나타냅니다. OPT는 캐시 optimization을 위한 이론적 상한을 제공하는 이상적인 정책입니다. OPT는 최적의 캐싱을 달성하기 위해 정확한 미래 정보를 가져옵니다. 패럿은 주로 하드웨어 캐시에 초점을 맞춘 오프라인 이미테이션 학습 기반 캐싱 policy입니다. predefined trace 에서 opT를 실행하여 OPT의 동작을 모방할 수 있어야 한다고 합니다.

Implementation 부분입니다.
프로토타입이 offline training component와 온라인 캐시의 두 부분으로 구성되어 있다고 합니다.
고로 offline training component에 대한 설명을 먼저 하겠습니다.
offline training component는 캐시 추적과 함께 입력됩니다. 그리고 several modules이 있다고 하고, feature trace를 생성한다고 합니다. 그리고 모듈이 피처 벡터 trace를 생성하는데요. 이는 데이터 샘플을 생성하는데 사용된다고 합니다. 그리하여 이러한 offline training component는 RNN 모델을 교육합니다.
그리고 online cache 부분입니다.
우리는 알고리즘 1을 따라 온라인 pOPT 캐시를 위한 시뮬레이터를 구현했습니다. pOPT 캐시는 온라인에서 forward reuse interval을 예측하는 cache trace를 통해 실행된다고 합니다
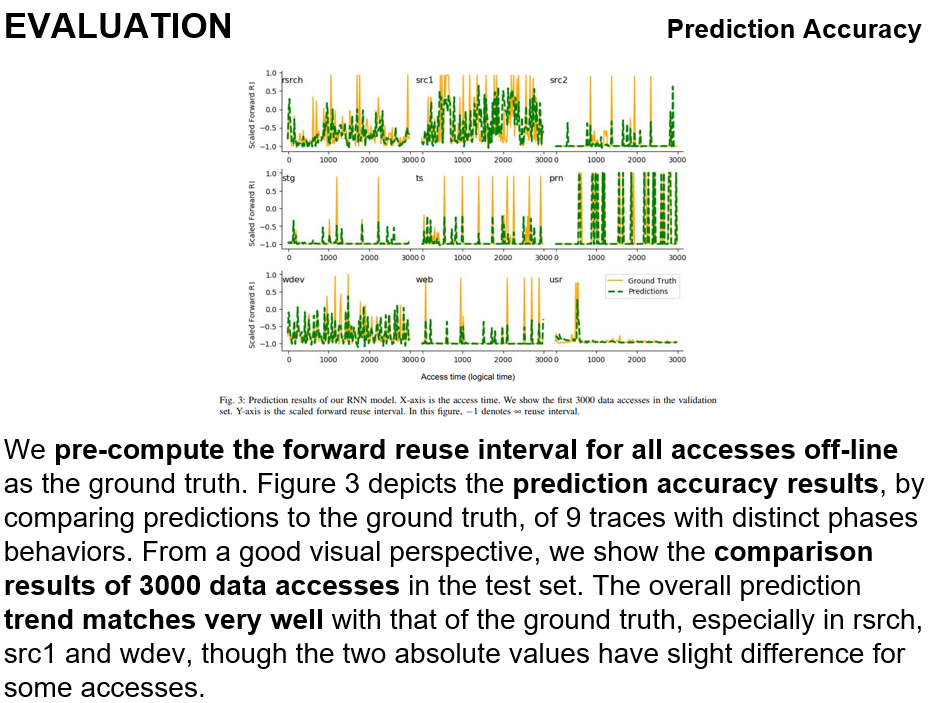
Prediction accuracy입니다.
우리는 모든 forward reuse interval을 먼저 계산합니다. 위 그림은 prediction accuracy results를 나타냅니다. 우리는 테스트 세트에서 3000개의 데이터 액세스의 비교 결과를 보여줍니다. 전체적인 예측 추세는 특히 rsrch, src1 및 wdev의 실제 예측 추세와 매우 잘 일치합니다.
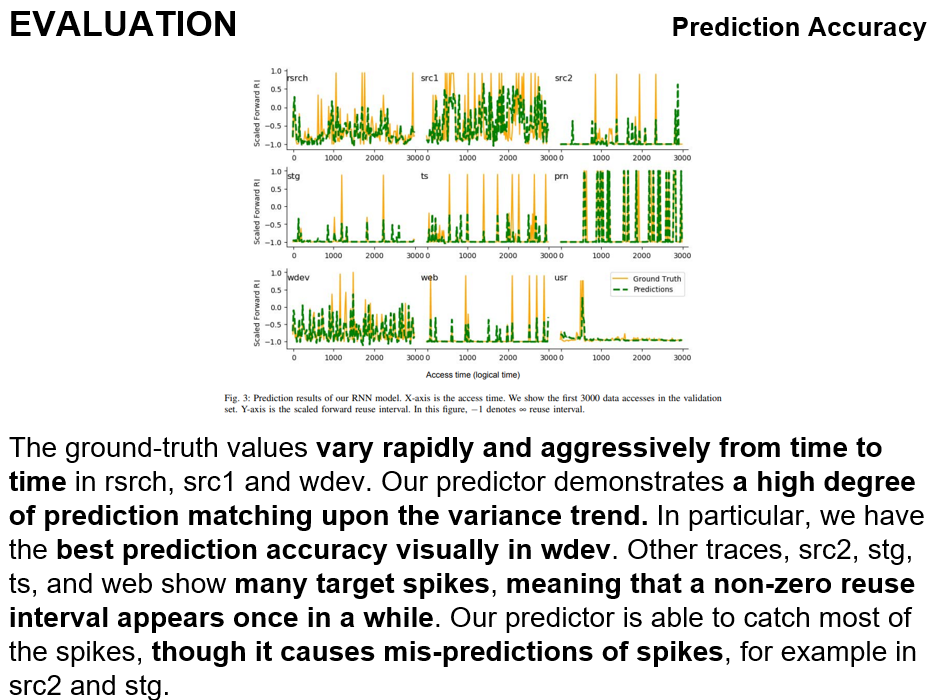
Ground-truth values는 rsrch, src1 및 wdev에서 수시로 빠르고 공격적으로 변화합니다. 그래도 우리의 예측기는 분산 추세에 대해서는 매우 높은 수준의 예측을 보여줍니다. 특히 우리는 wdev에서 시각적으로 최고의 예측 정확도를 가지고 있습니다. 그리고 src2, stg, ts, and web에서는 spike(커다란 못이라고 해석됨)에서 잘 예측하는 것을 보여 주는데요. 이는 0이 아닌 reuse interval이 한 번씩 나타내는 것을 의미 한다고 합니다. 그러나 우리의 preditor이 대부분의 spike를 잡지만, src2나 stg에서는 spike를 잘 예측못하는 경향이 있습니다
그 밖에 rmse점수로 보았을 때 잘 했다고 합니다.
그리고 위 그림은 우리의 예측 변수가 different data locality patterns and phase behaviors를 잘 예측한다는 것으로 결론을 냅니다
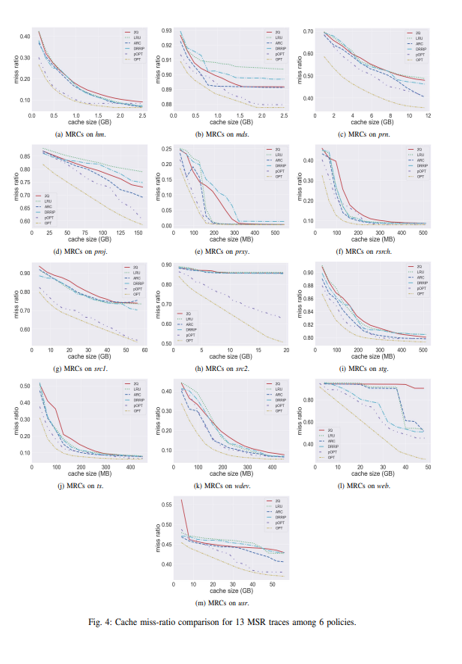
Fig 4입니다. 6개의 policies에 대한 Cache miss-ratio comparison for 13 miss ratio curves traces라고 합니다. 한편 opt는 정확한 미래 정보를 사용하고 pOPT는 예측된 미래 정보를 사용합니다. 그래서 차이가 있고 차이를 설명하는 것이 이번 챕터의 주 내용입니다..
pOPT가 hm, prxy, src1에서 OPT와 거의 유사한 성능을 보이지만 prn, proj, src2에서는 pOPT와 OPT 사이에 큰 차이가 있습니다.
모든 테스트에서 pOPT는 평균적으로 OPT보다 2.3% 높은 미스 비율을 가진다고 합니다. 그렇지만 캐시 크기가 매우 클 때는 pOPT는 최상의 미스 비율을 달성하는데 실패한다고 합니다.
그리고 한 번 더 캐시 크기가 증가할 때 miss rate의 감소를 나타낸다고 합니다
pOPT는 모든 테스트에서 평균적으로 LRU, 2Q 및 ARC보다 13.7%, 19.2%, 8.6% 더 우수합니다. 그리고 계속 다른 policies보다 우수하다고 합니다.
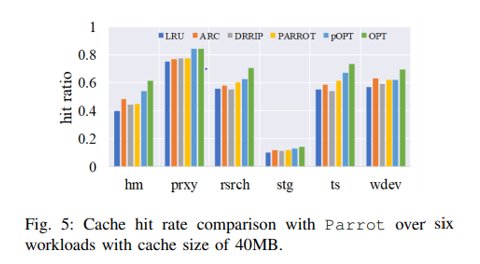
Figure 5는 6개의 트레이스에 대한 패럿과의 성능 비교를 보여줍니다. Parrot은 캐시가 크면 학습하는데 매우 오래 걸린다고 하기에 캐시 크기 40mb에서 학습을 했다고 하고요. 결론적으로 pOPT보다 성능이 떨어지지만, LRU ARC등 기존 policies보다는 우수한 성능을 보인다고 합니다
그리고 pOPT의 교차 모델 성능을 측정하고 personalized models와 비교합니다. 다음 장부터 나올 pOPT-hybrid와 pOPT-cross에 대한 개념을 먼저 설명 드리겠습니다.
첫 번째 모델인 pOPT-hybrid는 워크로드(특정 시간 내에 수행해야 하는 작업의 양)당 200,000개의 샘플을 통합하여 구성된 교육 세트로 훈련되고 모든 워크로드에 대한 테스트 샘플에 대해 개별적으로 검증된다. 두 번째 모델인 pOPT-cross는 상호 참조 모델로, 일부 워크로드에서 워크로드당 200,000개의 샘플을 선택하고 나머지 워크로드에 대해 검증함으로써 학습한다고 합니다.
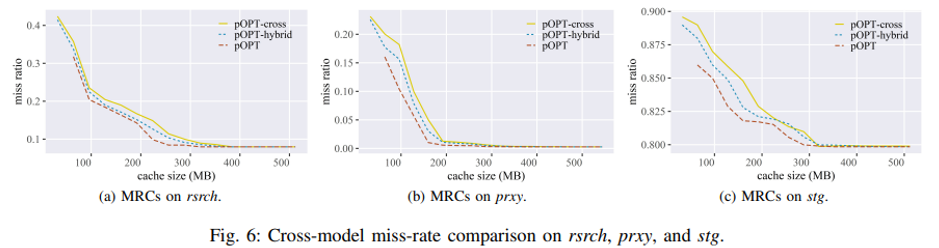
그림 6은 pOPT, pOPT-hybrid 및 pOPT-cross 사이에서 rsrch, prxy 및 stg에 대한 성능 비교를 보여준다. 놀랍게도 유니파이드 모델은 다양한 워크로드에서 일관성 있게 성능을 발휘할 뿐만 아니라 개인화된 모델만큼 경쟁력 있는 성능을 보여줍니다.
그러나, cross-reference 모델은 교육 및 검증 데이터의 데이터 패턴 불일치로 인해 약간 더 나쁜 성능을 보이지만, 여전히 기존 policy보다 더 우수하다고 합니다
게다가 캐시 miss rate performance 측면에서 모든 테스트에 대해 pOPT 하이브리드 및 pOPT 크로스를 LRU, 2Q 및 ARC와 비교한다고 합니다. 결론적으로 pOPT와 pOPT hybrid, pOPT cross는 모든 테스트에서 lRU 2Q ARC보다 효율적이라고 합니다
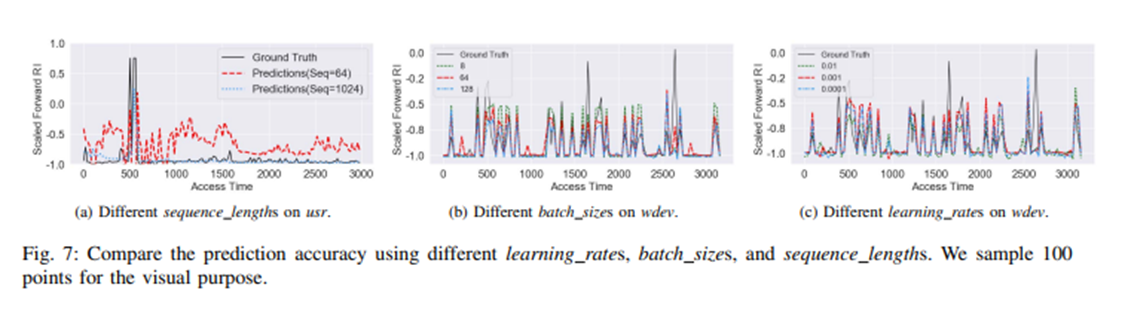
그리고 하이퍼 파라미터 부분입니다. 시퀀스 길이가 클수록 LSTM은 더 많은 과거 프로그램 동작을 기억하고 예측을 더 정확하게 할 수 있다라고 하며 시퀀스가 1024일때 0.88, 64일 때 0.65로 훨씬 우수하다는 것을 보여줍니다
여러 하이퍼 파라미터를 조정했고 배치 크기는 큰 영향을 미치지 않았다는 내용과 학습률이 0.01일때는 너무 커서 0.001과 0.0001사이에서 예측했다고 합니다. 다음 장에 배치 크기 및 학습률에 대한 자세한 정보를 소개합니다.
r-squared 점수로 배치 크기가 8일 때 0.91, 64일 때 0.90, 128일 때 0.90으로 거의 차이가 없고 학습률 0.01일때는 0.78로 낮은 수치를 보이지만 0.001일 때 0.91, 0.0001일 때 0.90으로 높은 수치를 기록하며 0.001과 0.0001 사이엔 거의 차이가 없는 것을 보여줍니다. 그리고 lstm width와 layer, epoch에서는 적당한 값을 취했다고 합니다
Lstm이 systems problem의 application에서 인기를 얻고 있다고 합니다. 컴파일러에 lstm 모델을 적용했다고 합니다. 또한 사전 추출을 최적화 하기 위해 객체 액세스 패턴을 학습하기 위해 lstm을 사용했다고 합니다. Parrot 또한 lstm모델을 사용하는 하드웨어 캐시에 초점을 맞추고 있다고 합니다.
CONCLUSION
본 논문에서, 우리는 전방 재사용 간격을 예측하기 위해 딥 러닝의 first use를 소개했습니다. 그리고 높은 예측 정확도를 달성하기 위해 LSTM 기반 RNNa locality driven feature 를 제시했다. 또한 pOPT replacement policy를 구현했습니다. 테스트에서 popt policy는 practical state-of-the-art policy을 최대 19.2% 능가하고 OPT에 근접한 미스 레이트 성능을 달성하는 것으로 입증되었습니다. 결론적으로 pOPT의 cross program prediction이 매우 경쟁력 있는 미스 비율 성능을 달성할 수 있음을 보여주었다고 합니다.