코드:
|
#include <iostream>
#include <math.h>
#define fastio() ios::sync_with_stdio(0),cin.tie(nullptr),cout.tie(nullptr);
using namespace std;
typedef long long ll;
ll n, m, k, from;
ll arr[10000000];
void update(ll location, ll v) {
ll idx = location + from - 1;
arr[idx] = v;
for (ll i = idx / 2; i >= 1; i /= 2) {
arr[i] = arr[i * 2] + arr[i * 2 + 1];
}
}
ll sum(ll l, ll r, ll idx = 1, ll L = 1, ll R = from) {
if (l > R or r < L) return 0;
else if (l <= L and r >= R) return arr[idx];
ll m = (L + R) / 2;
return sum(l, r, idx * 2, L, m) + sum(l, r, idx * 2 + 1, m + 1, R);
}
int main() {
fastio();
cin >> n >> m >> k;
from = ((n & (n - 1)) == 0) ? pow(2, (int)log2(n)) : pow(2, (int)log2(n) + 1);
for (ll i = from; i < from + n; i++) cin >> arr[i];
for (ll i = from - 1; i >= 1; --i) arr[i] = arr[i * 2] + arr[i * 2 + 1];
for (ll i = 0; i < m + k; i++) {
ll a, b, c;
cin >> a >> b >> c;
if (a == 1) {
update(b, c);
}
else {
cout << sum(b, c) << "\n";
}
}
}
|
cs |
용도:
값의 수정이 필요한 구간 합을 O(logN)으로 구할 때 사용합니다
자료구조 이해 1:

위 완전이진트리를 보면 리프노드의 합이 부모노드에 쓰인 걸 볼 수 있습니다
이러한 성질을 이용해서 구간합을 구할 때 부모노드를 이용하면, 구간합을 빨리 구할 수 있습니다
예를들어 초록색 리프 노드의 가장 왼쪽에 있는 5부터 가장 오른쪽에 있는 15까지 더한 값은 얼마일까요?

5부터 15까지를 일일이 더할 필요 없이, 루트노드에 80이 적혀 있으니 답을 구할 수 있습니다
그렇다면 5부터 8까지 더한 값은 얼마일까요?

마찬가지로 5부터 8까지 더할 필요 없이 부모노드를 참고하여 26을 얻을 수 있습니다
그렇다면 6부터 8까지 더한 값은 어떻게 알 수 있을까요?

6은 어쩔 수 없이 리프노드에 있는 값을 더해야 하지만, 7 + 8의 값은 부모노드에 15가 저장 되어있으므로, 검은줄이 그어진 6 + 15 = 21을 구할 수 있습니다
마찬가지 방법으로 6부터 14까지 더한 값은 얼마일까요?

6과 14를 더한 후 7 + 8, 12 + 13은 알고 있으므로, 검은 줄이 그어진 6 + 15 + 25 + 14 = 60을 리턴하면 됩니다
이와 같은 방법으로 구간합을 구할 시, 최고 높이가 logN인 완전이진트리이므로 O(logN)를 보장합니다
자료구조 이해 2:
그리고 세그먼트트리는 값을 수정하는 것도 O(logN)을 보장합니다.

위 세그먼트 트리에서 8을 1로 변경해 보겠습니다
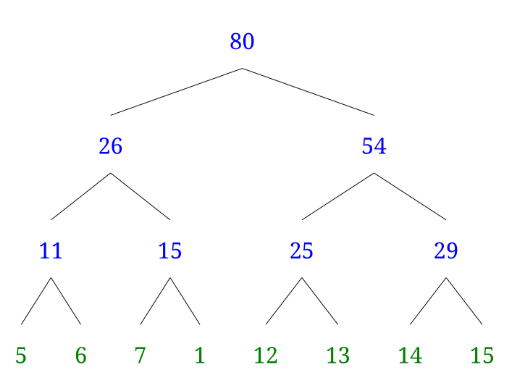
그런데 이렇게 변형한다면 7와 1의 부모를 15라고 하는 문제점이 생깁니다.
이 문제점을 해결해야 할 것입니다
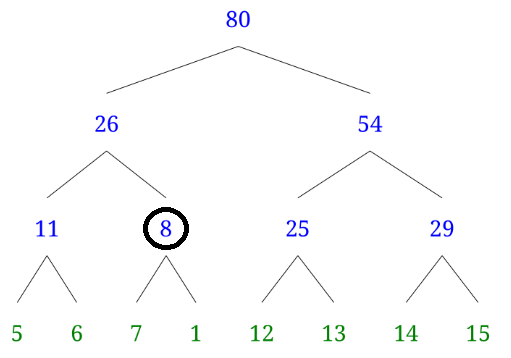
또 11와 8의 부모를 26이라고 하는 문제점이 생기며, 루트노드도 80이 아니니 바꾸어 주어야 할 것입니다.
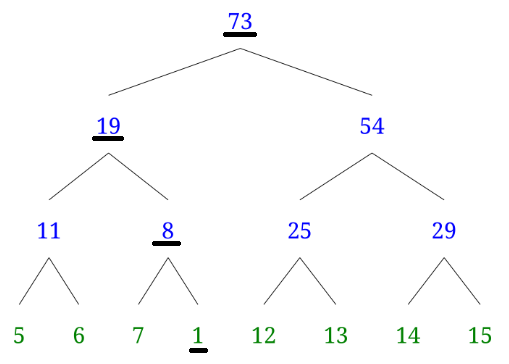
전부 수정한다면 다음과 같은 완전이진트리가 될 것입니다
이를 바탕으로 값을 수정하는 데 O(logN)의 시간복잡도를 가집니다.
코드 이해:
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
위 문제로 세그먼트 트리의 코드를 이해해 보겠습니다
|
#include <iostream>
#include <math.h>
#define fastio() ios::sync_with_stdio(0),cin.tie(nullptr),cout.tie(nullptr);
using namespace std;
typedef long long ll;
ll n, m, k, from;
ll arr[10000000];
void update(ll location, ll v) {
ll idx = location + from - 1; // n번째 값은 from - 1 뒤에 있으므로, idx를 구해줍니다
arr[idx] = v; // 값을 수정합니다
for (ll i = idx / 2; i >= 1; i /= 2) {
arr[i] = arr[i * 2] + arr[i * 2 + 1]; // 부모 노드의 값을 수정합니다
}
}
ll sum(ll l, ll r, ll idx = 1, ll L = 1, ll R = from) {
if (l > R or r < L) return 0; // 범위를 벗어났다면 0을 리턴합니다
else if (l <= L and r >= R) return arr[idx]; // 범위 안에 있다면 값을 리턴합니다
ll m = (L + R) / 2;
return sum(l, r, idx * 2, L, m) + sum(l, r, idx * 2 + 1, m + 1, R); // 3. 범위 안에 있는 자식들의 값을 리턴합니다
}
int main() {
fastio();
cin >> n >> m >> k;
from = ((n & (n - 1)) == 0) ? pow(2, (int)log2(n)) : pow(2, (int)log2(n) + 1); // 1. 완전이진트리의 값을 넣을 시작점을 구합니다
for (ll i = from; i < from + n; i++) cin >> arr[i]; // 구한 값부터 데이터를 넣어줍니다
for (ll i = from - 1; i >= 1; --i) arr[i] = arr[i * 2] + arr[i * 2 + 1]; // 2. 부모노드에 양 자식노드를 더한 값을 넣어줍니다
for (ll i = 0; i < m + k; i++) {
ll a, b, c;
cin >> a >> b >> c;
if (a == 1) {
update(b, c); // 값을 수정해 줍니다
}
else {
cout << sum(b, c) << "\n"; // 구간 합을 구합니다
}
}
}
|
cs |
Main 함수
1. 완전이진트리의 값을 넣을 시작점을 구합니다
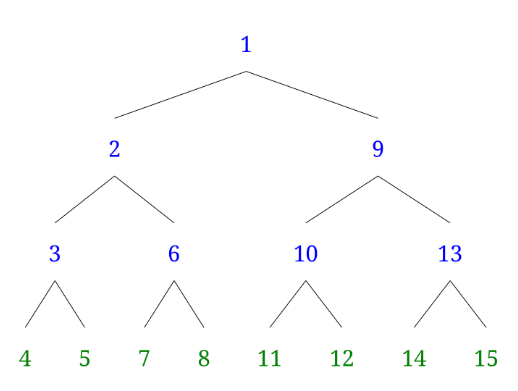
위는 세그먼트 트리가 아닌 완전이진트리입니다. 초록색 리프노드에 8개의 데이터를 넣는데 15개의 메모리가 필요합니다. 이를 식으로 옮기면
from = ((n & (n - 1)) == 0) ? pow(2, (int)log2(n)) : pow(2, (int)log2(n) + 1);가 될 것입니다.
1-1 만약 입력값 N이 2^n이 아니라면
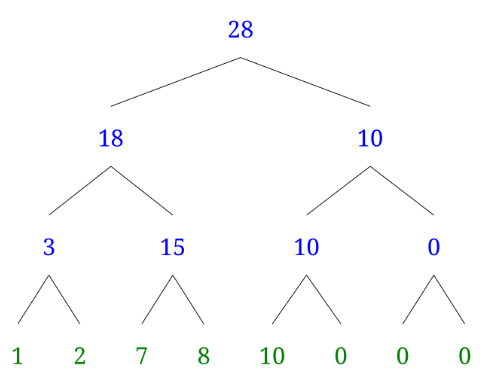
2^n이 아닐 때 2^n < N < 2^(n + 1)일 경우, from을 2^n + 1 로 잡고 입력이 되지 않는 부분은 0을 삽입하면 됩니다
2. 부모노드에 양 자식 노드를 더한 값을 넣어줍니다
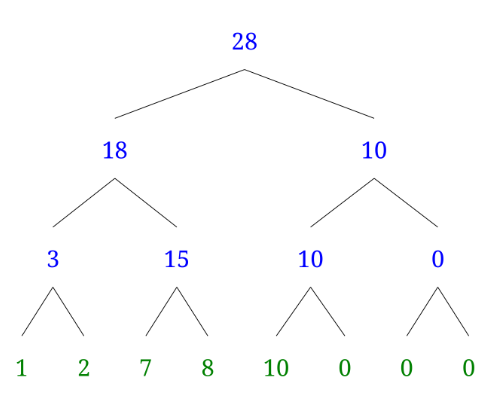
부모노드에 양 자식 노드의 더한 값을 넣어줘야 합니다
이를 배열로 나타낼 시 arr[] = {0, 28, 18, 10, 3, 15 ,10, 0, 1, 2, 7, 8, 10, 0, 0, 0}; 이므로
아래의 코드가 자명하다는 것을 알 수 있습니다.
for (ll i = from - 1; i >= 1; --i) arr[i] = arr[i * 2] + arr[i * 2 + 1];
ll sum(ll l, ll r, ll idx = 1, ll L = 1, ll R = from) 함수
3. 범위 안에 있는 자식들의 값을 리턴합니다.
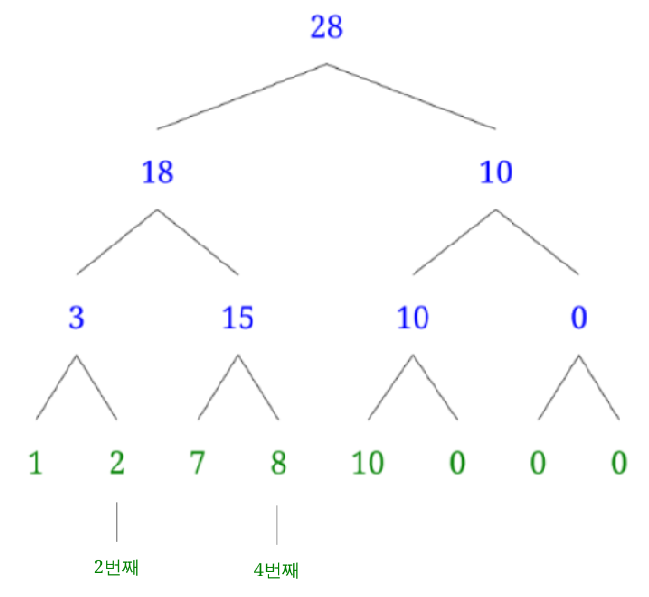
위 트리에서 2번째 노드부터 4번째 노드까지의 합을 구한다고 생각해 보면,
sum(2,4,1,1,8)을 메인에서 호출할 것입니다.
|
if (l > R or r < L) return 0;
else if (l <= L and r >= R) return arr[idx];
ll m = (L + R) / 2;
return sum(l, r, idx * 2, L, m) + sum(l, r, idx * 2 + 1, m + 1, R);
|
cs |
호출한다면
sum(2,4,1,1,8)은 if 조건도 else if 조건도 만족하지 못하기에
sum(2,4,2,1,4) + sum(2,4,3,5,8)을 리턴합니다
sum(2,4,2,1,4)는
sum(2,4,4,1,2) + sum(2,4,5,3,4)를 리턴합니다
sum(2,4,4,1,2)는
sum(2,4,8,1,1)+sum(2,4,9,2,2)를 리턴합니다
sum(2,4,8,1,1)은 if 조건을 만족하기에
0을 리턴합니다
sum(2,4,9,2,2)는 elseif 조건을 만족하기에
2를 리턴합니다
2를 리턴합니다
sum(2,4,5,3,4)는 elseif조건을 만족하기에
15를 리턴합니다
17을 리턴합니다
sum(2,4,3,5,8)은 if 조건을 만족하기에
0을 리턴합니다
17을 리턴합니다
17을 리턴합니다
와 같이 진행됩니다.
void update(ll location, ll v)함수
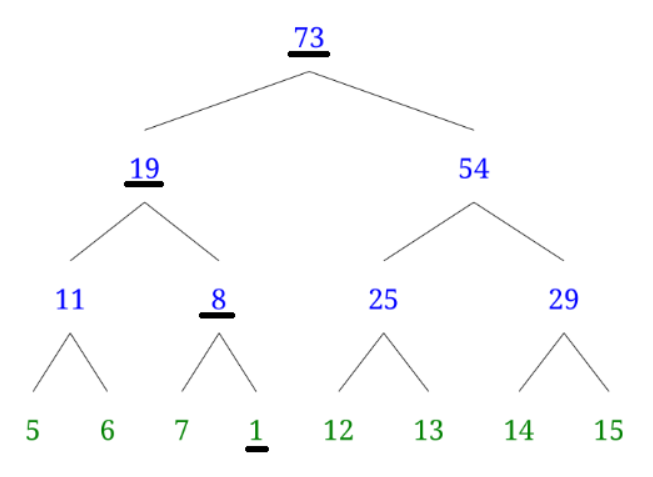
이전과 똑같이 진행됩니다. 코드를 보시면 어렵지 않을 겁니다
|
#include <iostream>
#include <math.h>
#define fastio() ios::sync_with_stdio(0),cin.tie(nullptr),cout.tie(nullptr);
using namespace std;
typedef long long ll;
ll n, m, k, from;
ll arr[10000000];
void update(ll location, ll v) {
ll idx = location + from - 1;
arr[idx] = v;
for (ll i = idx / 2; i >= 1; i /= 2) {
arr[i] = arr[i * 2] + arr[i * 2 + 1];
}
}
ll sum(ll l, ll r, ll idx = 1, ll L = 1, ll R = from) {
if (l > R or r < L) return 0;
else if (l <= L and r >= R) return arr[idx];
ll m = (L + R) / 2;
return sum(l, r, idx * 2, L, m) + sum(l, r, idx * 2 + 1, m + 1, R);
}
int main() {
fastio();
cin >> n >> m >> k;
from = ((n & (n - 1)) == 0) ? pow(2, (int)log2(n)) : pow(2, (int)log2(n) + 1);
for (ll i = from; i < from + n; i++) cin >> arr[i];
for (ll i = from - 1; i >= 1; --i) arr[i] = arr[i * 2] + arr[i * 2 + 1];
for (ll i = 0; i < m + k; i++) {
ll a, b, c;
cin >> a >> b >> c;
if (a == 1) {
update(b, c);
}
else {
cout << sum(b, c) << "\n";
}
}
}
|
cs |
문제 1:
https://www.acmicpc.net/problem/11505
11505번: 구간 곱 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
답 1:
https://wantchicken.tistory.com/47
백준 11505 구간 곱 구하기
https://www.acmicpc.net/problem/11505 11505번: 구간 곱 구하기 첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K..
wantchicken.tistory.com
문제 2:
https://www.acmicpc.net/problem/2357
2357번: 최솟값과 최댓값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수, 또는 제일 큰 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100
www.acmicpc.net
답 2:
https://wantchicken.tistory.com/48
백준 11505 구간 곱 구하기
https://www.acmicpc.net/problem/11505 11505번: 구간 곱 구하기 첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K..
wantchicken.tistory.com
'알고리즘 - 기초' 카테고리의 다른 글
| N-Queens Problem C++ Code BackTracking (0) | 2022.06.17 |
|---|---|
| 게임이론 기초, c++ (0) | 2022.06.03 |
| 하노이 탑 파이썬 - 재귀 함수를 사용해 보자 (0) | 2022.06.02 |
| linkedList를 이용한 LIS 역 추적, 백준 14003-가장 긴 증가하는 부분 수열 5 [C/C++] (0) | 2022.05.26 |
| 다이나믹 프로그래밍 - 기초 (0) | 2022.05.26 |